Newtonian Quantum Dot
This paper studies definitions related to coherent states and their connections to path integrals. We will make use some derived definitions and apply it to the path integral formulation. The derivation of the coherent state propagator will resemble that of the ordinary path integral propagator, with the exception of the usage of an alternative form of the completeness relation in the language of coherent state. The coherent state path integral is particularly useful for defining bosonic and fermionic path integrals. It serves as a useful method to convert, with the knowledge of the Hamiltonian of the system, the Hamiltonian into the Lagrangian of the action.
Definition 1 ∀k The eigenvalues of the creation and annihilation operators can be expressed as
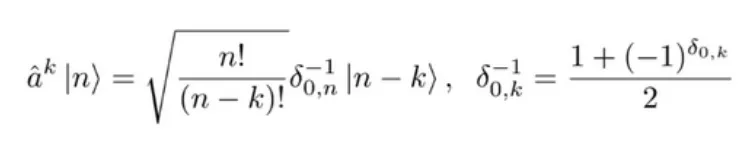
First Propagator: Klauder and Skagerstan
The propagator derived in this section will not contain time dependent complex parameter, as we shall see in the next section. This one was already derived by Klauder and Skagerstan. Thus, we insert n-1 copies of the completeness relation into the propagator,

Second Propagator: Time Dependence
In this section, we focus on building time dependence in our variables such that we arrive at answers that involve derivatives. In particular, we generate time dependence in the Heisenberg’s picture by incorporating time dependence in the creation and annihilation operators such that the states shifted by it will be associated with some time dependent function such that the coherent state vector will depend on time but will not be shifted into Shrodinger’s picture. Now, we induce the following definition:
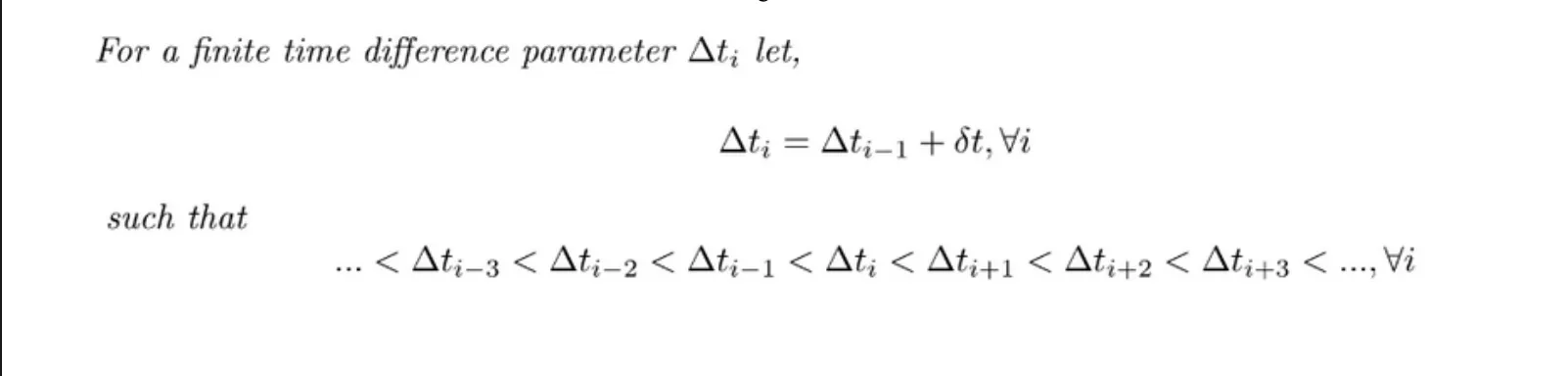
We parameterize β as follows:
We begin by parameterizing the creation and annihilation operator as,

Alongside with the definitions, we have provided a general concept on the mathematical analysis of time dependent coherent state path integrals and its Lagrangian.
